Контрольная работа № 1.

Номера задач выбираются в соответствии с двумя последними цифрами номера зачетной книжки студента на пересечении соответствующей строки с соответствующим столбцом из таблицы 1 – для контрольной работы № 1.

Все программы в контрольных работах должны начинаться с комментария, в котором указываются фамилия, инициалы, номер зачетной книжки студента и номер выполняемой задачи.

Контрольную работу следует оформлять на листах формата А4. На обложке должны быть указаны: название дисциплины, номер группы, шифр (номер зачетной книжки), фамилия и инициалы студента. Тексты программ должны быть приведены в виде распечаток, остальную часть работы можно выполнять от руки. Также нужно сделать распечатку копии экрана с пользовательской формой и (или) рабочего листа с исходными данными и результатами.

В конце каждой работы следует приводить список использованной литературы.

Таблица 1 – Варианты задач для контрольной работы № 1

Предпоследняя цифра номера зачетной книжки	Последняя цифра номера зачетной книжки
	9	8	7	6	5	4	3	2	1	0
9	1, 17 33,53,73,93,113, 133	11, 27 43,63,83, 103, 123, 143	4, 29 35,55,75,95,115, 135	9, 25 50,70,90, 110, 130, 150	6, 21 39,59,79,99,119, 139	7, 24 33,52,72,92,112, 132	3, 20 43,62,82, 102, 122, 142	11, 28 48,68,88, 108, 128, 148	1, 26 36,56,76,96,126, 146	6, 30 48,67,87, 107, 127, 147
8	12, 21 50,69,89, 109, 129, 149	2, 18 34,64,84, 104, 124, 144	12, 28 44,54,74,94, 114, 134	5, 28 37,57,77,97,117, 137	11, 27 48,66,86, 106, 126, 136	8, 23 37,56,75,94, 113, 132	8, 25 34,53,72,91,120, 139	4, 21 44,63, 81,99, 107, 125	12, 29 41,61,81, 101, 121, 141	3, 27 35,53,72,91, 110, 138
7	8, 26 41,60,79,98, 117, 136	13, 20 48,65, 109, 117, 126, 145	3, 19 35,53,71,89,107, 125, 143	13, 29 45,65,85, 105, 125, 148	6, 27 39,58, 77,96, 115, 134	15, 29 46,66,85, 104, 133, 142	10, 25 35,54,70,88, 116, 146	9, 26 36,55, 74,93, 112, 131	5, 22 45,64,83, 102, 121, 144	13, 30 40,59,78, 108, 126, 139
6	7, 24 33,49, 81,97, 123, 139	10, 24 40,60,80, 100, 120, 140	14, 19 46,77,81, 114, 136, 144	4, 20 36,57,78,99, 120, 141	14, 30 47,67,87, 107, 127, 147	7, 26 41,63,84, 105, 126, 147	15, 31 45,46,67,88, 109, 130	12, 27 33,54,75,96, 111, 138	10, 27 35,56, 77,98, 119, 140	6, 23 46,67, 88, 109, 130, 150
5	1, 18 46,68,90, 112, 134, 148	9, 26 35,77,99, 121, 143, 150	12, 22 39,60, 81, 103, 125, 147	15, 18 44,55,76,97,118, 139	5, 21 37,58,79, 100, 121, 142	15, 31 46,69,92, 115, 138, 144	8, 25 43,65,77,99,121, 143	2, 32 44,66,88, 110, 132, 149	14, 29 50,64,76,81, 115, 140	11, 28 37,48,59,80,100, 135
4	12, 29 38,59,77,93, 124, 141	2, 19 44,59,82, 100, 128, 148	11, 28 49,60,91, 108, 122, 137	14, 20 38,48,78,99, 123, 144	16, 17 42,58,77,85,111, 131	6, 22 38,57,70,98,116, 138	16, 32 48,54, 66, 103, 123, 145	9, 24 45,55,67,92, 118, 146	4, 30 43,56,72,88,105, 142	16, 31 48,57,68,79,104, 146
3	7, 24 47,67,99, 115, 131, 147	13, 30 39,84,100, 116, 132, 148	3,20 42,69, 85, 101, 117, 133	13, 30 47,70,86, 102, 118, 149	16, 18 37,55,71,87, 119, 135	1, 17 56,72,88, 104, 120, 136	7, 23 39,73,89, 105, 121, 137	1, 32 49,58,90, 106, 122, 138	10, 23 47,59, 75,91,107, 139	6, 28 42,60, 92, 108, 124, 140
2	14, 31 39,61,93, 109, 125, 141	8, 25 48,61,77, 110, 126, 142	14, 31 41,63,95, 111, 127, 143	4, 21 40,62,78, 112, 128, 144	15, 32 45, 64,80, 96, 129, 145	1, 18 36,62,78,94, 128, 146	3, 19 38,65, 81,97, 113, 147	8, 24 40,62,78,94, 114, 136	2, 31 50,68,85, 102, 119, 137	11, 22 49,70,87, 104, 120, 138
1	4, 28 34,51,83, 101, 118, 134	15, 32 38,56,73,90, 124, 148	9, 26 49,77,94, 111, 128, 145	15, 17 40,52,76,95,130, 150	5, 22 38,46,91, 117, 134, 149	2, 17 43,54,74,94, 127, 144	3, 20 35,66,84,99,119, 149	5, 21 36,79, 92, 110, 127, 148	9, 25 41,53,91, 107, 124, 141	3, 30 33,59,79, 110, 130, 143
0	7, 31 44,68,92, 119, 136, 149	5, 29 33,57, 81, 105, 117, 142	16, 25 37,48, 54,67,115, 146	10, 27 50,70,80, 103 125, 142	2, 19 42,65,84,91, 126, 148	6, 23 36,54,75,88,114, 132	4, 19 41,64,78,95, 121, 145	5, 22 46,59,83, 102, 119, 139	7, 23 34,49,67,92, 111, 134	10, 26 42,60,90, 123, 137, 150

Варианты задач для контрольной работы № 1

1 Требования к выполнению задач:

1) указать какие имена (идентификаторы) были присвоены переменным. Для задач сначала следует записать расчетные формулы и сделать математическое обоснование;

2) написать программу на языке VISUAL BASIC FOR APPLICATIONS (VBA), где значения переменных, входящих в выражение, вводятся через пользовательскую форму или из рабочего листа EXCEL, а результаты счета выводятся на пользовательскую форму(если она есть) и на рабочий лист EXCEL;

3) указать, какие стандартные функции и операторы языка программирования VBA были использованы.

2 Условия задач

1. Определить конечные значения переменных X и Y в результате выполнения следующих алгоритмов:

2. Числа а и b — катеты одного треугольника, с и d — катеты другого.

Определить являются ли эти треугольники равновеликими.

3. Вычислить значение выражения (все переменные имеют действительный тип)

4. Заданы координаты вершин прямоугольника:

Определить площадь части прямоугольника, расположенной в 1-й координатной четверти.

5. Написать программу, которая по номеру дня недели (натуральному числу от 1 до 7) выдает в качестве результата количество уроков в Вашем классе в этот день.

6. Дано натуральное число п. Вычислить:

S=1! + 2! + 3! + ... + n! (n>1).

7. Дан массив натуральных чисел. Найти сумму элементов, кратных данному К.

8. Дана вещественная матрица размером n x m. Переставить ее наибольший элемент (или один из max) в верхний левый угол.

9. Треугольник задан координатами своих вершин. Составить программу вычисления его площади.

10. В строке имеется одна точка с запятой (;). Подсчитать количество символов до точки с запятой и после нее.

11. Вычислить периметр и площадь прямоугольного треугольника по заданным длинам двух катетов а и b.

12. Составить программу, печатающую значение TRUE, если указанное высказывание является истинным, и FALSE в противном случае:

13. данное натуральное число а кратно числу b, но не кратно числу с. Чила а, b и c вводятся.

14. Даны три действительные числа. Возвести в квадрат те из них, значения которых неотрицательны, и в четвертую степень — отрицательные.

15. . Дан массив натуральных чисел. Найти сумму элементов, кратных данному К.

16. Составить программу, которая печатает TRUE, если точка с координатами (x,y) принадлежит заштрихованной области, и FALSE в противном случае

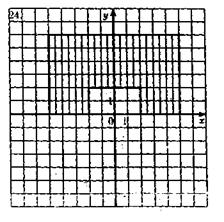
17. Определить значение целочисленной переменной S после выполнения алгоритмов:

S:=128

для i от 1 до 4 повторять

нц

S := S - 3

кц

18. Последовательно вводятся N целых чисел. Найт минимальное из положительных значений.

19. Вычислить значения выражения (все переменные имеют действительный тип).

20. Полторы кошки за полтора часа съедают полторы мышки.

Сколько мышек съедят Х кошек за Y часов?

21. Составить программу, печатающую значение TRUE, если указанное высказывание является истинным, и FALSE в противном случае.

22. Среди чисел a, b, c есть хотя бы одна пара взаимно противоположных чисел.

23. Написать программу нахождения суммы большего и меньшего из 3 чисел..

24. Даны три числа а, b, с. Определить, какое из них равно d. Если ни одно не равно d, то найти max (d-a, d-b, d-c).

25. Составить программу, позволяющую по последней цифре данного числа определить последнюю цифру куба этого числа.

26. Составить программу, печатающую значение TRUE, если точка с координатами (x, y) принадлежит заштрихованной области, и FALSE в противном случае.

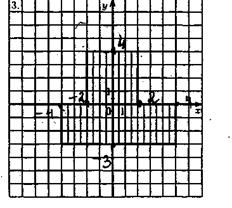
27. Одноклеточная амеба каждые 3 часа делится на 2 клетки. Определит, сколько амеб будет через 3, 6, 9, 12, ..., 24 часа.

28. Определить наименьший элемент каждой четной строки матрицы А[М, N].

29. Найдите сумму цифр заданного натурального числа.

30. Имеется строка, содержащая буквы латинского алфавита и цифры. Вывести на экран длину наибольшей последовательности цифр, идущих подряд.

31. Угол а задан в градусах, минутах и секундах. Найти его величину в радианах (с максимально возможной точностью).

32. Перевести заданную величину угла из радианной меры в градусную.

33. Длина отрезка задана в дюймах (1дюйм=2,54 см). Перевести значение длины в метрическую систему, т.е. выразить ее в метрах, сантиметрах и миллиметрах.

34. Заданы моменты начала и конца некоторого промежутка времени в часах, минутах и секундах (в пределах одних суток). Найти продолжительность этого промежутка в тех же единицах измерения.

35. За первый год производительность труда на предприятии возросла на p₁%, за второй и третий – соответственно на p₂% и p₃%. Найти среднегодовой прирост производительности (в процентах).

36. Найти площадь сектора радиуса r, а дуга содержит заданное число радиан j.

37. Заданы три корня кубического уравнения. Найти коэффициенты этого уравнения.

38. Заданы действительная и мнимые части комплексного числа z=x+іy. Преобразовать его в тригонометрическую форму и напечатать в виде выражения z=r(cosφ+isinφ).

39. Найти корни квадратного уравнения, заданного своими коэффициентами, с положительным дискриминантом; вывести погрешность вычислений для каждого корня.

40. Заданы уравнения двух пересекающихся прямых на плоскости: y=k₁+b₁; y=k₂+b₂. Найти (в градусах и минутах) угол между ними, используя формулу tga=(k₂-k₁)/(1+k₁k₂).

41. 1 верста=500 саженей; 1 сажень=3 аршина; 1 аршин= 16 вершков; 1 вершок=44,45 мм. Длина некоторого отрезка составляет p метров. Перевести ее в русскую неметрическую систему.

42. У квадрата ABCD на плоскости известны координаты двух противоположных вершин – точек A и C. Найти координаты точек B и D.

43. Треугольник ABC задан длинами своих сторон. Найти длину высоты, опущенной из вершины A.

44. Найти координаты вершины параболы, y=ax²+bx+c.

45. Функция y=sinx на отрезке [0;π/2] хорошо аппроксимируется разложением: y=x-x³/6+x⁵/120. Для заданного значения аргумента x вычислить y по этой формуле и сравнить (вывести) с точным значением, вычисленным с помощью стандартной функции Sin.

46. Треугольник задается координатами своих вершин на плоскости: A(x₁;y₁), B(x₂;y₂), C(x₃;y₃). Найти площадь треугольника ABC.

47. Треугольник задается координатами своих вершин на плоскости: A(x₁;y₁), B(x₂;y₂), C(x₃;y₃). Найти периметр треугольника ABC.

48. Треугольник задается координатами своих вершин на плоскости: A(x₁;y₁), B(x₂;y₂), C(x₃;y₃). Найти сумму длин медиан треугольника.

49. Треугольник задается координатами своих вершин на плоскости: A(x₁;y₁), B(x₂;y₂), C(x₃;y₃). Найти длину и основание высоты, опущенной из вершины A на сторону BC.

50. Найти площадь равнобедренной трапеции с основаниями a и b и углом при основании a.

51. Известна длина окружности. Найти площадь круга, ограниченного этой окружностью.

52. Даны гипотенуза и катет прямоугольного треугольника. Найти второй каткт и радиус вписанной окружности.

53. Найти сумму n членов арифметической прогрессии по известным первому члену и разности этой прогрессии.

54. Треугольник задан длинами своих сторон. Определить длины всех его высот.

55. Найти площадь кольца, внешний радиус которого R, а внутренний r.

56. Треугольник задается координатами своих вершин на плоскости: A(x₁;y₁), B(x₂;y₂), C(x₃;y₃). Найти точку D симметричную точке A относительно стороны BC.

57. Треугольник задается координатами своих вершин на плоскости: A(x₁;y₁), B(x₂;y₂), C(x₃;y₃). Найти внутренние углы (в градусах) треугольника.

58. Треугольник задается координатами своих вершин на плоскости: A(x₁;y₁), B(x₂;y₂), C(x₃;y₃). Найти точку пересечения биссектрис (центр вписанной окружности).

59. Треугольник задается координатами своих вершин на плоскости: A(x₁;y₁), B(x₂;y₂), C(x₃;y₃). Найти точку пересечения медиан треугольника.

60. Трехмерные векторы заданы своими координатами, например, ā (x_a;y_a;z_a). Найти угол (в градусах) между векторами ā и .

61. Пройдет ли кирпич со сторонами a,b,c сквозь прямоугольное отверстие со сторонами r,s? Стороны отверстия должны быть параллельны граням кирпича.

62. Может ли шар радиуса r пройти через ромбообразное отверстие с диагоналями p и q.

63. Можно ли коробку размером a´b´c упаковать в посылку размером r´s´t? «Углом» укладывать нельзя.

64. Можно ли из круглой заготовки радиуса r вырезать две прямоугольные пластинки с размерами a´b и c´d?

65. Можно ли на прямоугольном участке застройки размером a на b метров разместить два дома размером в плане p на q и r на s метров? Дома можно располагать только параллельно сторонам участка.

66. Проверить, лежит ли окружность (x-a₁)²+(y-b₁)²=R₁ целиком внутри окружности (x-a₂)²+(y-b₂)²=R₂ или наоборот.

67. Лежит ли точка M(x_m;y_m) внутри треугольника, заданного координатами своих вершин на плоскости?

68. Два отрезка на плоскости заданы координатами своих концов. Определить имеют ли эти отрезки общие точки.

69. Среди трех заданных чисел найти пары кратных.

70. Как известно, число делиться на 3 тогда и только тогда, когда сумма его цифр делится на 3. Используя данный признак проверить делиться ли данное число на 3.

71. Можно ехать на такси со скоростью v₁ км/ч и оплатой p₁ р./км либо идти пешком со скоростью v₂ км/ч и оплатой p₂ р./км. Как с наименьшими затратами преодолеть путь s за время t, если это возможно? Каковы эти затраты?

72. Суточный рацион коровы составляет u кг сена, v кг силоса и w кг комбикорма. В хозяйстве, содержащем k голов, осталось s центнеров сена, t тонн силоса и f мешков сена по 50 кг. Сколько еще дней хозяйство сможет прокормить коров по полному рациону? Какой из кормов кончится раньше других?

73. Банк предлагает три вида срочных вкладов: на 3 месяца под р%, на 6 месяцеи под к% и на год под t%. Какой из вкладов наиболее выгоден для вкладчика?

74. Для заданного 0£n£120, рассматриваемого как возраст человека, вывести фразу вида: “Мне 21 год”, “Мне 32 года”, “Мне 12 лет”.

75. Из круга какого наименьшего радиуса можно вырезать треугольник со сторонами a, b, c?

76. Даны действительные числа x, y, z. Проверить, могут ли данные числа являть длинами сторон треугольника. В случае положительного результата, проверить является ли он прямоугольным.

77. Даны действительные числа x, y, z. Проверить, могут ли данные числа являть длинами сторон треугольника. В случае положительного результата, определить его вид (разносторонний, равносторонний или равнобедренный).

78. Даны действительные числа a, b, c, d. Если a£b£c£d, то каждое число заменить наибольшим из них; если a>b>c>d, то числа оставить без изменения, в противном случае все числа заменяются их квадратами.

79. Даны действительные числа a, b, c (a¹0). Решить биквадратное уравнение ax⁴+bx²+c=0 (при наличии комплексных корней записать их в виде x=s+ti).

80. Найти действительные корни уравнения ax²+bx+c=0.

81. Два треугольника задаются координатами своих вершин. Выяснить, лежит ли первый треугольник внутри другого.

82. Четыре точки на плоскости задаются своими координатами. Проверить, могут ли они являться вершинами квадрата.

83. Четыре точки на плоскости задаются своими координатами. Проверить, могут ли они являться вершинами прямоугольника.

84. Четыре точки на плоскости задаются своими координатами. Проверить, могут ли они являться вершинами трапеции.

85. Четыре точки на плоскости задаются своими координатами. Проверить, могут ли они являться вершинами параллелограмма.

86. Четыре точки на плоскости задаются своими координатами. Проверить, могут ли они являться вершинами равнобедренной трапеции.

87. Четыре точки на плоскости задаются своими координатами. Проверить, могут ли они являться вершинами ромба.

88. Четырехугольник ABCD задан координатами своих вершин. Проверить является ли он выпуклым.

89. Два треугольника задаются длинами своих сторон. Проверить, являются ли данные треугольники подобными.

90. Вводится дата рождения человека (число и месяц). Определить его знак по гороскопу.

91. В массиве С(n) подсчитать количество отрицательных элементов и сумму положительных элементов.

92. От каждого из m чисел отнять их среднее арифметическое (использовать только один одномерный массив).

93. Вычислить среднее значение и дисперсию для заданного массива X(k) наблюдений:

.

94. Многочлены P_m(x) и Q_n(x) заданы массивами своих коэффициентов. Найти частное и остаток от деления P_m(x) на Q_n(x) (в виде массивов коэффициентов).

95. Каждый элемент вектора A(n) (кроме двух крайних) заменить выражением:

, а крайние элементы – выражениями:

.

96. Удалить из массива A(n) нулевые элементы, передвинув на их место следующие элементы без нарушения порядка их следования. В результате должен получиться массив меньшего размера, не содержащий нулей.

97. В массиве K(n) в порядке убывания представлены достоинства денежных знаков (купюр и монет) валютной системы некоторой страны. Реализовать выдачу в этой системе заданной суммы m минимальным числом денежных знаков.

98. В массиве A(n) наименьший элемент поместить на первое место, наименьший из оставшихся – на последнее место, следующий по величине – на второе место, следующий – на предпоследнее и так далее до середины массива.

99. Удалить в заданном массиве X(n) «лишние» (кроме первого) элементы так, чтобы оставшиеся образовывали возрастающую последовательность (за один просмотр массива).

100. В массиве A(n) каждый третий элемент заменить полусуммой двух предыдущих, а стоящий перед ним – полусуммой соседних с ним элементов. Дополнительный (рабочий) массив не использовать.

101. В массиве H(t) найти первый и последний нулевые элементы.

102. В массиве Р(t) найти наиболее длинную цепочку нулей.

103. Даны два целочисленных массива R(m) и L(n). Найти наибольший элемент массива R, не имеющий себе равных в массиве L.

104. В целочисленном массиве A(n) найти наиболее длинную цепочку одинаковых подряд стоящих элементов.

105. В массиве A(n) много совпадающих элементов. Найти количество различных элементов (не упорядочивая массива).

106. Найти все числа, встречающиеся в массиве A(m) строго два раза (не упорядочивая массива).

107. В массиве A(n) найти самую длинную последовательность, которая является арифметической прогрессией.

108. В массиве A(n) найти самую длинную последовательность, которая является геометрической прогрессией.

109. В массиве A(2n+1), не содержащем одинаковых элементов, найти средний по величине элемент, т.е. такой, что в массиве А ровно n элементов меньших его и столько же элементов больше его. Массив А сохранить (не сортировать), дополнительных массивов не использовать.

110. Задан массив, состоящий из n неотрицательных элементов. Найти в нем индекс элемента, для которого сумма элементов, стоящих до него, наименее отличается от суммы элементов, стоящих после него.

111. Дан массив целых чисел. Найти в нем максимальный и минимальный элементы. Вывести все элементы исходного массива, расположенные (находящиеся) между этими экстремальными значениями.

112. Дан массив целых чисел. Найти в нем максимальный (max) и минимальный (min) элементы. Вывести в порядке возрастания все целые числа из интервала (max;min).

113. В массиве A(n) вывести номера (индексы) локальных максимумов, т.е. таких a_i, что a_i-1<a_i>a_i+1.

114. В массиве A(2n) каждый элемент с четными индексами поменять местами с предыдущим.

115. Многочлен P_n(x) задан массивом своих коэффициентов A(n+1). Найти массив коэффициентов производной этого многочлена.

116. В массиве Z(n) найти число чередований знака, т.е. число переходов с минуса на плюс или с плюса на минус (нуль знака не имеет).

117. В массиве А(n) каждый элемент, кроме первого, заменить суммой всех предыдущих элементов.

118. Каждый из элементов массива X(n) x_i заменить средним значением первых i элементов этого массива.

119. Каждый из элементов массива Х(n) x_i заменить минимальным среди первых i элементов этого массива.

120. Осуществить циклический сдвиг элементов массива T(n) на m позиций влево (при этом необязательно m<n).

121. Элементы одномерного массива A(n²) построчно расположить в матрице B(n,n).

122. Строки матрицы A(m,n) заполнены не полностью: в массиве L(m) указано количество элементов в каждой строке. Переслать элементы матрицы построчно в начало одномерного массива T(m·n), подсчитать их количество.

123. Матрицу M(m,n) заполнить натуральными числами от 1 до m·n по спирали, начинающейся в верхнем левом углу и закрученной по часовой стрелке.

124. В матрице A(m,n) каждый элемент a_i,j заменить минимальным среди элементов подматрицы A^/(i,j), расположенной в левом верхнем углу матрицы А.

125. В матрице A(m,n) каждый элемент a_i,j заменить суммой элементов подматрицы A^/(i,j), расположенной в левом верхнем углу матрицы А.

126. Матрицу A(m,n) заполнить следующим образом: для заданных k и l элементу a_kl присвоить значение 1; элементам, окаймляющим его 9соседние элементы по вертикали, горизонтали и диагоналям) – значение 2; элементам следующего окаймления – значение 3 и так далее до заполнения всей матрицы.

127. Матрицу K(m,n) заполнить следующим образом: элементам, находящимся на периферии (по периметру матрицы), присвоить значение 1; периметру оставшейся подматрицы – значение 2 и так далее до заполнения всей матрицы.

128. В массиве X(m,n) каждый элемент (кроме граничных) заменить суммой непосредственно примыкающих к нему элементов по вертикали, горизонтали и диагоналям.

129. Содержимое квадратной матрицы А(n,n) повернуть на 90⁰ по часовой стрелке, считая центром поворота центр симметрии матрицы.

130. В каждом столбце и каждой строке матрицы P(n,n) содержится строго по одному нулевому элементу. Перестановкой строк добиться расположения всех нулей по главной диагонали матрицы.

131. Матрица A(n,n) состоит из нулей и единиц. Найти в ней номера хотя бы одной строки, не содержащей единицы.

132. Найти среднее арифметическое элементов каждой строки матрицы A(m,n) и вычесть его из элементов этой строки.

133. В матрице A(m,n) все ненулевые элементы заменить обратными по величине и противоположными по знаку.

134. Задана матрица A(k,l). Найти вектор B(l), каждый элемент которого равен среднему арифметическому элементов соответствующего столбца матрицы А.

135. Дан массив A(n,m). Все положительные его элементы поместить в начало массива B(n·m), а отрицательные – в начало массива C(n·m). Подсчитать количество тех и других.

136. Латинским квадратом порядка n называется квадратная таблица размером n·n, каждая строка и каждый столбец которой содержат все числа от 1 до n. Проверить является ли заданная целочисленная матрица латинским квадратом.

137. Латинским квадратом порядка n называется квадратная таблица размером n·n, каждая строка и каждый столбец которой содержат все числа от 1 до n. Организовать создание такой матрицы.

138. Магическим квадратом порядка n называется квадратная таблица размером n·n, состоящая из чисел 1,2,3,…,n² так, что сумма по каждому столбцу, каждой строке и каждой из двух диагоналей равны между собой. Проверить, является ли заданная целочисленная матрица магическим квадратом.

139. Седловой точкой в матрице называется элемент, являющийся одновременно наибольшим в столбце и наименьшим в строке. Седловых точек может быть несколько (в этом случае они имеют разные значения). В матрице А(n,m) найти седловую точку и ее координаты.

140. Дана матрица A(m,n). Сравнить сумму элементов нижней треугольной матрицы (элементы, стоящие ниже главной диагонали) с суммой элементов главной диагонали, не вычисляя суммы всех элементов исходной матрицы.

141. В каждой строке квадратной матрицы найти наибольший и поменять его с соответствующим диагональным.

142. Найти все числа, каждое из которых встречается в каждой строке матрицы A(m,n).

143. Проверить, не является ли заданная матрица A(m,n) осесимметричной.

144. Проверить, не является ли заданная матрица A(m,n) центросимметричной.

145. Заполнить матрицу A(m,n) числами 1,2,3,4, так, чтобы по горизонтали и вертикали не было одинаковых элементов.

146. Результаты сессии, состоящей из трех экзаменов, для группы из n студентов представлены матрицей K(n,3). Оценка ставится по пятибалльной системе; неявка обозначена единицей. Подсчитать количество неявок, неудовлетворительных, удовлетворительных, хороших и отличных оценок по каждому предмету.

147. Просуммировать элементы матрицы A(n,n) по каждой из линий, параллельных главной диагонали.

148. Для матрицы A(m,n) найти ее норму:

.

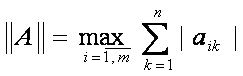149. В матрице A(m,n) найти минимальный среди максимальных элементов столбцов.

150. Дана матрица A(m,n). Определить разность наибольшего и наименьшего элементов в каждой строке.

3 Пример выполнения задания

Пусть требуется написать программу для решения следующей задачи:

Даны натуральные числа a, b и c. Могут ли эти числа быть углами треугольника и если могут, то является ли этот треугольник прямоугольным?

Сначала сделаем математическое обоснование задачи.

По теореме Пифагора мы знаем, что сумма углов любого треугольника равна 180 градусов, следовательно нам надо найти сумму этих чисел и сравнить ее с числом 180. Также известно, что треугольник является прямоугольным, если один из его углов равен 90 градусам.

Присвоим переменным идентификаторы

Переменная	a	b	c
Идентификатор	a	b	c

Программа для решения задачи будет иметь вид:

'Иванов И. И. Шифр 001234. Задача № 00

'Описание переменных на уровне модуля

Dim a As Integer

Dim b As Integer

Dim c As Integer

Dim rez As String

Private Sub CommandButton1_Click()

'Процедура обработки события при нажатии кнопки “ОК”

'Контроль ввода данных

If (IsNumeric(TextBox1.Text) = False) Or (IsNumeric(TextBox2.Text) = False) _

Or (IsNumeric(TextBox3.Text) = False) Then

MsgBox "Ошибка при вводе данных", vbCritical, "Сообщение об ошибке"

Exit Sub

End If

'Присвоение значений переменным

a = CInt(TextBox1.Text)

b = CInt(TextBox2.Text)

c = CInt(TextBox3.Text)

'Проверка чисел на положительность

If a <= 0 Or b <= 0 Or c <= 0 Then

MsgBox "Числа a, b и c должны быть положительными", vbCritical, _

"Сообщение об ошибке"

Exit Sub

End If

'Являются ли a, b и c углами треугольника

If (a + b + c = 180) And (a = 90 Or b = 90 Or c = 90) Then

rez = "Числа a,b,c являются углами прямоугольного треугольника"

ElseIf a + b + c = 180 Then

rez = "Числа a,b,c являются углами непрямоугольного треугольника"

Else

rez = "Числа a,b,c не являются углами треугольника"

End If

TextBox4.Visible = True

TextBox4.Text = rez

'Вызов процедуры пользователя

Vivod_na_list

End Sub

Private Sub CommandButton2_Click()

'Процедура обработки события при нажатии кнопки “Выход”

Unload UserForm1

End Sub

Private Sub Vivod_na_list()

'Процедура пользователя для вывода данных и результатов на рабочий лист EXCEL

With Worksheets("Лист1")

.Range("a1").Value = a

.Range("a2").Value = b

.Range("a3").Value = c

.Range("a4").Value = rez

End With

End Sub

При написании программы были использованы следующие стандартные функции языка программирования VBA:

IsNumeric()- проверка, является ли выражение в скобках числом

CInt()- преобразование выражения к целому типу Integer

Операторы :

-присваивания

-многострочный If в полной форме

Вид формы пользователя изображен на рис.1

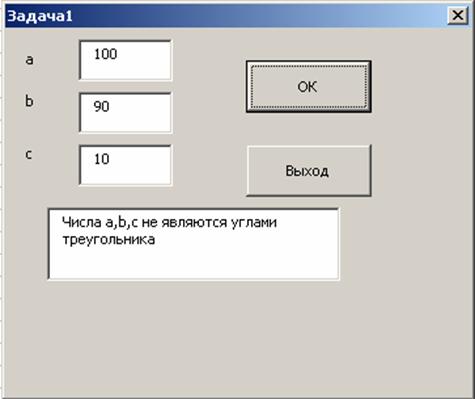
Рисунок 1. Пользовательская форма.

Результаты на рабочем листе EXCEL приведены на рис.2

100

90

10

Числа a,b,c не являются углами треугольника