Все формулы раздела- площадь фигур
Все формулы площади плоских фигур
Площадь эллипса
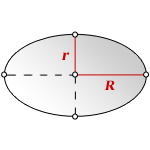
R - большая полуось
r - малая полуось
π ≈ 3.14
Формула площади эллипса, через полуоси:

Площадь равнобедренной трапеции
1. Формула площади равнобедренной трапеции через стороны и угол
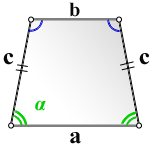
а - нижнее основание
b - верхнее основание
с - равные боковые стороны
α - угол при нижнем основании
Формула площади равнобедренной трапеции через стороны, (S ):
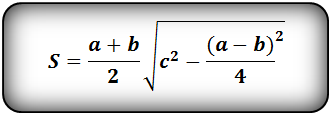
Формула площади равнобедренной трапеции через стороны и угол, (S ):
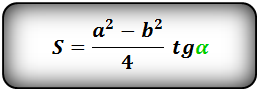
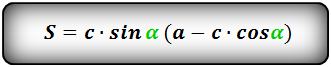
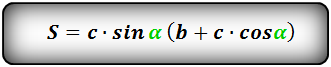
2. Формула площади равнобедренной трапеции через радиус вписанной окружности
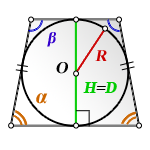
R - радиус вписанной окружности
D - диаметр вписанной окружности
O - центр вписанной окружности
H - высота трапеции
α, β - углы трапеции
Формула площади равнобедренной трапеции через радиус вписанной окружности, (S ):
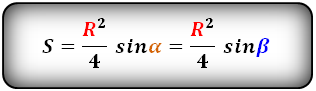
СПРАВЕДЛИВО, для вписанной окружности в равнобедренную трапецию:
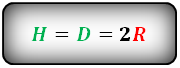
3. Формула площади равнобедренной трапеции через диагонали и угол между ними
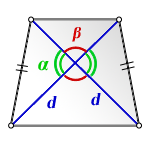
d - диагональ трапеции
α, β - углы между диагоналями
Формула площади равнобедренной трапеции через диагонали и угол между ними, (S ):
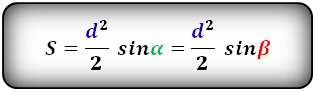
4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании
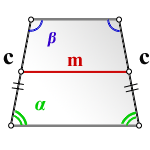
c - боковая сторона
m - средняя линия трапеции
α, β - углы при основании
Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании,
(S ):
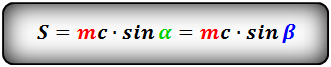
5. Формула площади равнобедренной трапеции через основания и высоту
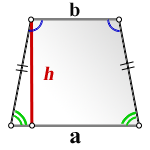
a - нижнее основание
b - верхнее основание
h - высота трапеции
Формула площади равнобедренной трапеции через основания и высоту, (S ):
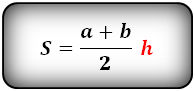
Площадь треугольника по стороне и двум углам, формула.
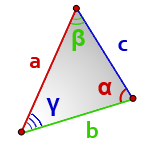
a, b, c- стороны треугольника
α, β, γ- противолежащие углы
Площадь треугольника через сторону и два угла (S):
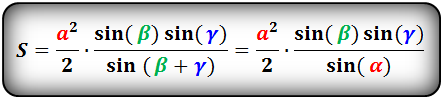
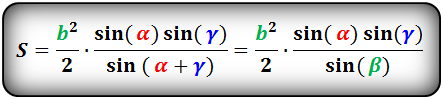
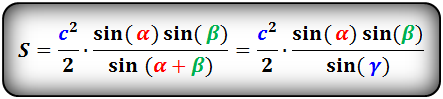
Формула площади правильного многоугольника
a - сторона многоугольника
n - количество сторон
Площадь правильного многоугольника, (S):

Площадь треугольника, формула Герона
a, b, c,- стороны треугольника
p- полупериметр, p=(a+b+c)/2
Формула (Герона) площади треугольника через полупериметр (S):

Формула расчета площади треугольника
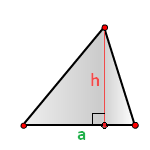
h - высота треугольника
a - основание
Площадь треугольника (S):
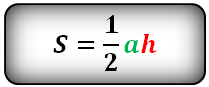
Площадь сектора кольца
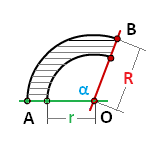
R - радиус внешней окружности
r - радиус внутренней окружности
α - угол сектора AOB, в градусах
π ≈ 3.14
Формула площади сектора кольца (S):

Площадь кольца
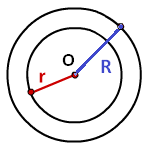
R - радиус внешней окружности
r - радиус внутренней окружности
π ≈ 3.14
Формула площади кольца (S):
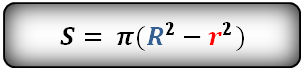
Площадь сегмента круга
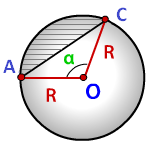
R - радиус круга
α - угол сегмента в градусах
π ≈ 3.14
Формула площади сегмента круга (S), отсекаемая хордой AC:
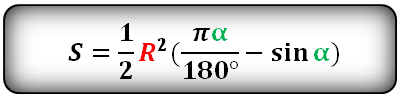
Площадь сектора круга
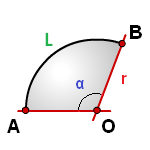
r - радиус круга
L - длина дуги AB
α - угол сектора круга AOB в градусах
π ≈ 3.14
Формула площади сектора круга (S), через длину дуги (L):
.png)
Формула площади сектора круга (S), через угол (α):
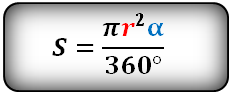
Вычислить площадь ромба
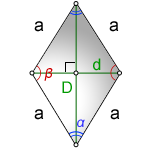 a - сторона ромба
a - сторона ромба
D - большая диагональ
d - меньшая диагональ
α - острый угол
β - тупой угол
Формулы площади ромба ( S ):
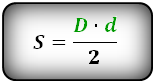
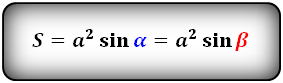
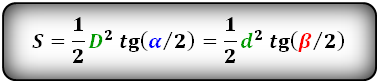
Формулы площади параллелограмма
1. Формула площади параллелограмма через стороны и углы
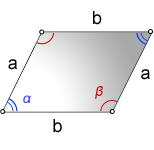
a, b - стороны параллелограмма
α, β - углы параллелограмма
Формула площади через стороны и углы параллелограмма, (S):

2. Формула площади параллелограмма через сторону и высоту
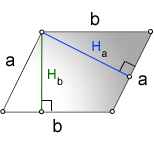
a, b - стороны параллелограмма
Hb - высота на сторону b
Ha - высота на сторону a
Формула площади через стороны и высоты параллелограмма, (S):
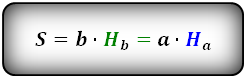
3. Формула площади параллелограмма через диагонали и угол между ними
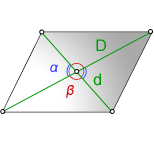
D - большая диагональ
d - меньшая диагональ
α, β - углы между диагоналями
Формула площади через диагонали параллелограмма и угол между ними , (S):
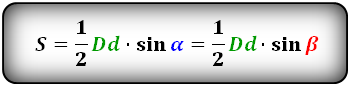
Найти площадь треугольника, угол и две стороны
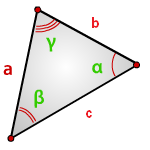
Зная у треугольника, две стороны и синус угла между ними, находим по формуле, его площадь.
a, b, c - стороны треугольника
α, β, γ - углы
Формулы площади треугольника, через две стороны и угол между ними, (S):
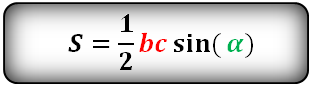
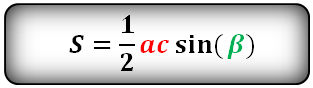
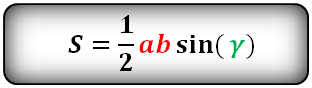
Площадь равностороннего треугольника равна:
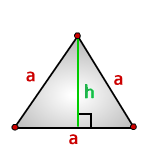
Формулы расчета, площади равностороннего треугольника.
a - сторона треугольника
h - высота
Площадь треугольника через сторону a и высоту h, (S):
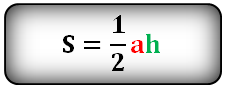
Площадь треугольника только через сторону a, (S):
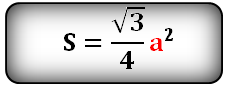
Площадь треугольника только через высоту h, (S):
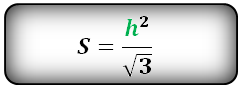
Как вычислить площадь равнобедренного треугольника ?
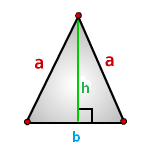
b - основание треугольника
a - равные стороны
h - высота
Формула площади треугольника через высоту h и основание b, (S):
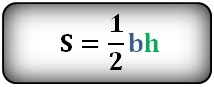
Формула площади треугольника через, стороны a, b, (S):

Площадь прямоугольного треугольника по катетам
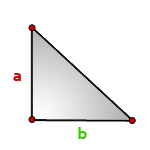
Зная катеты прямоугольного треугольника, можно по формуле, найти его площадь.
a, b - катеты треугольника
Формула площади прямоугольного треугольника, (S):
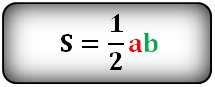
Площадь произвольной трапеции
1. Формула площади трапеции через основания и высоту
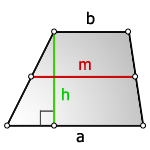
a - нижнее основание
b - верхнее основание
m - средняя линия
h - высота трапеции
Формула площади трапеции, (S ):
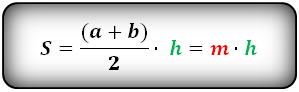
2. Формула площади трапеции через диагонали и угол между ними
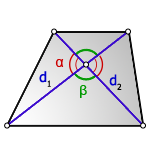
d1 , d2 - диагонали трапеции
α , β - углы между диагоналями
Формула площади трапеции, (S ):
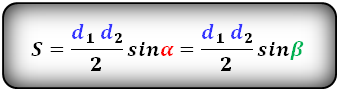
3. Формула площади трапеции через четыре стороны
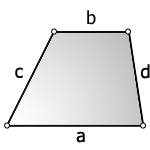
a - нижнее основание
b - верхнее основание
c , d - боковые стороны
Формула площади трапеции, (S ):

Как рассчитать площадь квадрата через диагональ или сторону
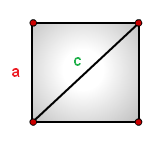
a - сторона квадрата
c - диагональ
Формула площади квадрата через сторону a, (S):

Формула площади квадрата через диагональ c, (S):
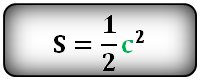
Формула расчета площади прямоугольника
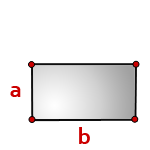
b - длина прямоугольника
a - ширина
Площадь прямоугольника, (S):

Формула площади круга, диаметр
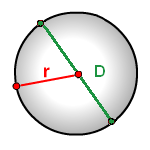
Зная диаметр или радиус круга, можно найти его площадь.
r - радиус круга
D - диаметр
π ≈ 3.14
Формула площади круга, (S):
.png)
Площадь плоских фигур
